Erhabene Zahl

Eine erhabene Zahl oder sublime Zahl ist eine natürliche Zahl ${\displaystyle n}$ mit der besonderen Eigenschaft, dass die Anzahl ihrer Teiler ${\displaystyle \tau (n)}$ und ihre Teilersumme ${\displaystyle \sigma (n)}$ vollkommene Zahlen sind. Bislang sind nur zwei erhabene Zahlen bekannt.

Bekannte erhabene Zahlen

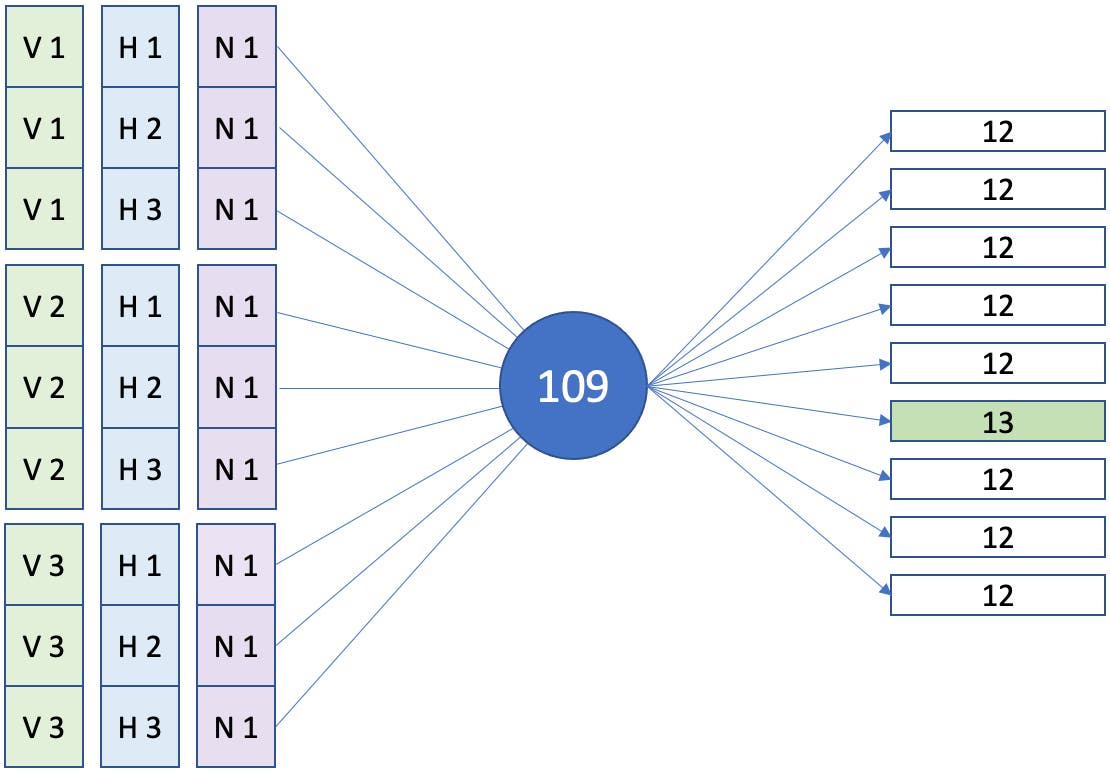
12

• Die 12 hat 6 Teiler: 12, 6, 4, 3, 2, 1.
• Die Summe ihrer Teiler beträgt: 1 2 3 4 6 12 = 28.

${\displaystyle \tau (12)=6}$ und ${\displaystyle \sigma (12)=28}$ sind vollkommene Zahlen.

6.086.555.670.238.378.989.670.371.734.243.169.622.657.830.773.351.885.970.528.324.860.512.791.691.264

6086555670238378989670371734243169622657830773351885970528324860512791691264 = 2¹²⁶ (2⁶¹ − 1)(2³¹ − 1)(2¹⁹ − 1)(2⁷ − 1)(2⁵ − 1)(2³ − 1).
Diese 76-stellige erhabene Zahl wurde von Kevin Brown entdeckt.

• Die Anzahl der Teiler ist: (126 1) 2⁶ = 8128.
• Die Summe der Teiler ist: (2^{126 1}-1) 2^{61 31 19 7 5 3} = (2¹²⁷-1) 2¹²⁶.

${\displaystyle \tau (60865556\dotso )=(2^{7}-1)2^{6}=8128}$ und ${\displaystyle \sigma (60865556\dotso )=(2^{127}-1)2^{126}}$ sind vollkommene Zahlen.

Es ist nicht bekannt, ob noch weitere erhabene Zahlen existieren oder ob es unendlich viele oder auch ungerade erhabene Zahlen geben könnte.

Literatur

• Clifford A. Pickover: Dr. Googols wundersame Welt der Zahlen. Deutscher Taschenbuch-Verlag, München 2005, ISBN 3-423-34177-7. 
• Jean-Marie De Koninck: Those Fascinating Numbers. American Mathematical Society, Providence 2009, ISBN 978-0-8218-4807-4, S. 4 (online) und S. 395 (online).

Siehe auch

• Liste besonderer Zahlen

Weblinks

• Sublime Numbers auf mathpages.com

Einzelnachweise