Deming-Regression

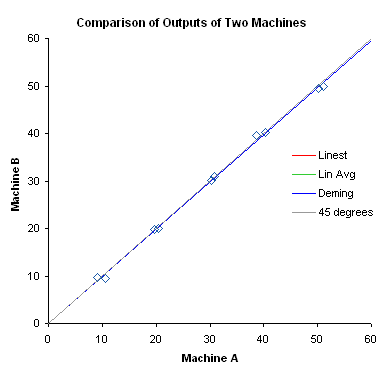
In der Statistik wird mit der Deming-Regression eine Ausgleichsgerade für eine endliche Menge metrisch skalierter Datenpaare (${\displaystyle x_{i},y_{i}}$) nach der Methode der kleinsten Quadrate bestimmt. Es handelt sich um eine Variante der linearen Regression. Bei der Deming-Regression werden die Residuen (Messfehler) sowohl für die ${\displaystyle x}$- als auch für die ${\displaystyle y}$-Werte in das Modell einbezogen.

Die Deming-Regression ist somit ein Spezialfall der Regressionsanalyse; sie beruht auf einer Maximum-Likelihood-Schätzung der Regressionsparameter, bei der die Residuen beider Variablen als unabhängig und normalverteilt angenommen werden und der Quotient ${\displaystyle \delta }$ ihrer Varianzen als bekannt unterstellt wird.

Die Deming-Regression geht auf eine Arbeit von C.H. Kummell (1879) zurück; 1937 wurde die Methode von T.C. Koopmans wieder aufgegriffen und in allgemeinerem Rahmen 1943 von W. E. Deming für technische und ökonomische Anwendungen bekannt gemacht.

Die orthogonale Regression ist ein wichtiger Spezialfall der Deming-Regression; sie behandelt den Fall ${\displaystyle \delta =1}$. Die Deming-Regression wiederum ist ein Spezialfall der York-Regression.

Rechenweg

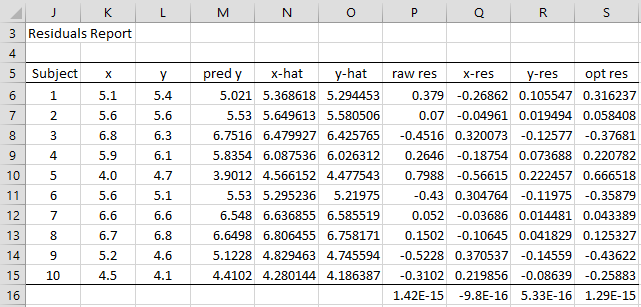
Die gemessenen Werte ${\displaystyle x_{i}}$ und ${\displaystyle y_{i}}$ werden als Summen der „wahren Werte“ ${\displaystyle x_{i}^{*}}$ bzw. ${\displaystyle y_{i}^{*}}$ und der „Fehler“ ${\displaystyle \eta _{i}}$ bzw. ${\displaystyle \varepsilon _{i}}$ aufgefasst, d. h. ${\displaystyle (x_{i},y_{i})=(x_{i}^{*} \eta _{i},y_{i}^{*} \varepsilon _{i})}$ Die Datenpaare (${\displaystyle x_{i}^{*},y_{i}^{*}}$) liegen auf der zu berechnenden Geraden. ${\displaystyle \eta _{i}}$ und ${\displaystyle \varepsilon _{i}}$ seien unabhängig mit ${\displaystyle \sigma _{\eta }^{2}:=Var(\eta )}$ und ${\displaystyle \sigma _{\varepsilon }^{2}:=Var(\varepsilon )}$. Bekannt sei zumindest der Quotient der Fehlervarianzen ${\displaystyle \delta ={\frac {\sigma _{\eta }^{2}}{\sigma _{\varepsilon }^{2}}}}$.

Es wird eine Gerade

${\displaystyle y=\beta _{0} \beta _{1}x}$

gesucht, die die gewichtete Residuenquadratsumme minimiert:

${\displaystyle SQR=\sum _{i=1}^{n}{\bigg (}{\frac {\eta _{i}^{2}}{\sigma _{\eta }^{2}}} {\frac {\varepsilon _{i}^{2}}{\sigma _{\varepsilon }^{2}}}{\bigg )}={\frac {1}{\sigma _{\varepsilon }^{2}}}\sum _{i=1}^{n}{\Big (}(y_{i}-\beta _{0}-\beta _{1}x_{i}^{*})^{2} \delta (x_{i}-x_{i}^{*})^{2}{\Big )}\ \to \ \min _{\beta _{0},\beta _{1},x_{i}^{*}}SQR}$

Für die weitere Rechnung werden die folgenden Hilfswerte benötigt:

${\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$     (arithmetisches Mittel der ${\displaystyle x_{i}}$)

${\displaystyle {\overline {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$     (arithmetisches Mittel der ${\displaystyle y_{i}}$)

${\displaystyle s_{x}^{2}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$     (Stichprobenvarianz der ${\displaystyle x_{i}}$)

${\displaystyle s_{y}^{2}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}$     (Stichprobenvarianz der ${\displaystyle y_{i}}$)

${\displaystyle s_{xy}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}$     (Stichprobenkovarianz der ${\displaystyle (x_{i},y_{i})}$).

Damit ergeben sich die Parameter zur Lösung des Minimierungsproblems:

${\displaystyle \beta _{1}={\frac {s_{y}^{2}-\delta s_{x}^{2} {\sqrt {(s_{y}^{2}-\delta s_{x}^{2})^{2} 4\delta s_{xy}^{2}}}}{2s_{xy}}}}$

${\displaystyle \beta _{0}={\overline {y}}-\beta _{1}{\overline {x}}}$.

Die ${\displaystyle x_{i}^{*}}$-Koordinaten berechnet man mit

${\displaystyle x_{i}^{*}=x_{i} {\frac {\beta _{1}}{\beta _{1}^{2} \delta }}(y_{i}-\beta _{0}-\beta _{1}x_{i})}$.

Erweiterung York-Regression

York-Regression erweitert die Deming-Regression, da es korrelierte x- und y-Fehler erlaubt.

Einzelnachweise