Szintillation (Strahlungsphysik)

Szintillation (von lat. scintillare ‚funkeln‘, ‚flackern‘) beschreibt in der Physik der kondensierten Materie einen Vorgang, bei dem eine als Szintillator bezeichnete Substanz ultraviolettes oder sichtbares Licht ausstrahlt unter Anregung durch hoch-energetische Photonen (Röntgen- oder Gammastrahlung) oder durch energiereiche Teilchen (wie Elektronen, Alphateilchen, Neutronen oder Ionen).

Grundlagen

Szintillation ist eine Form von Lumineszenz, bei der ein charakteristisches Spektrum an Licht in Folge von Strahlungsanregung emittiert wird. Der Szintillationsprozess kann zusammengefasst werden in drei Schritten: Wechselwirkung, Energie-Transfer zum Lumineszenz-Zentrum und Lumineszenz.

Die abgegebene Strahlung enthält üblicherweise weniger Energie als die aufgenommene. Szintillation ist deshalb im Allgemeinen ein "down-conversion"-Prozess.

Wechselwirkung

Die erste Stufe der Szintillation ist die Wechselwirkung der Energie des eintreffenden Teilchens oder Photons mit dem Szintillator-Material. Dabei entstehen hoch-energetische Elektronen und Löcher. Die Art der Wechselwirkung im Szintillator hängt ab von der Art der Teilchen und deren Energie.

Freie, bewegte Moleküle, Atome oder Elementarteilchen (z. B. Alpha-, Betateilchen, Neutronen), ionisieren Atome oder Moleküle des Szintillators.

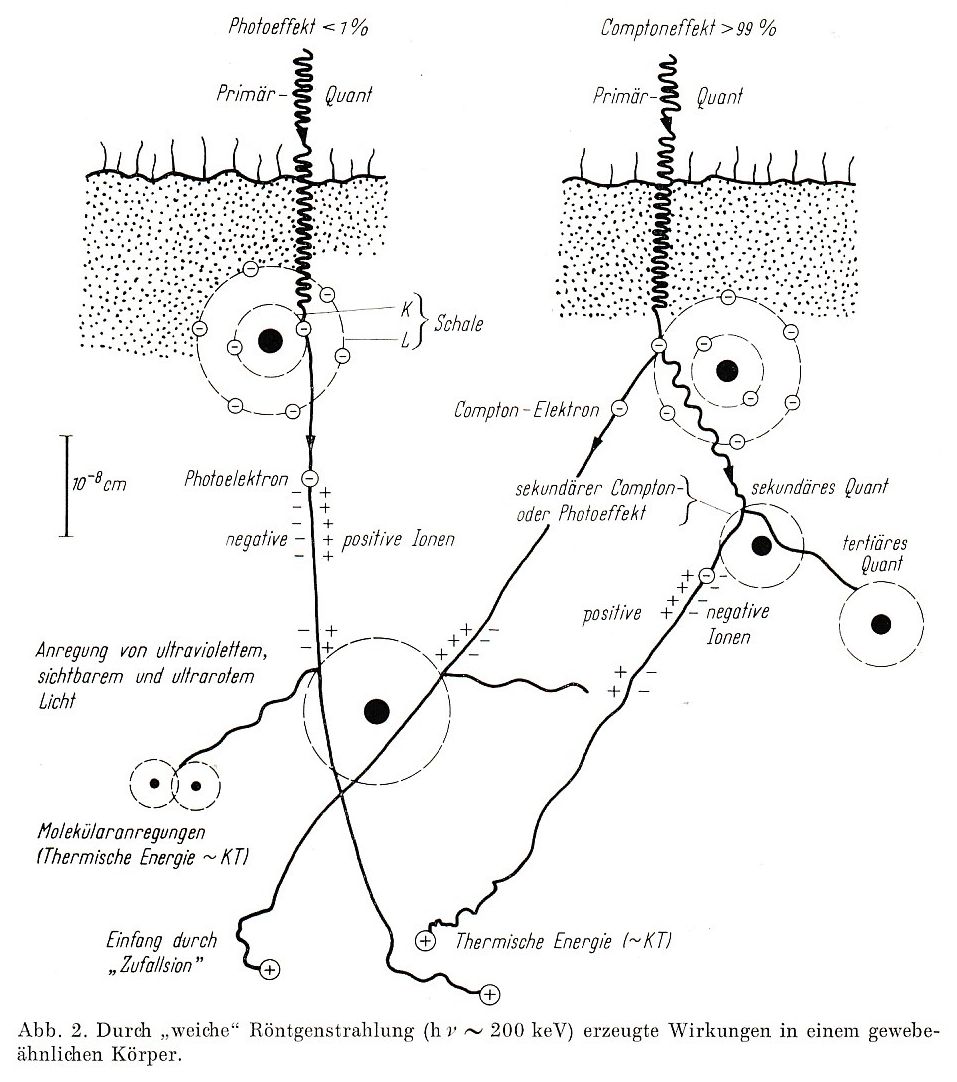
Für hoch-energetische Photonen wie Röntgen- (0,1 keV < $E_{\gamma }$ < 100 keV) und Gammastrahlen ( $E_{\gamma }$ > 100 keV) existieren drei Mechanismen zur Energieumwandlung:

Photoelektrischer Effekt
Compton-Effekt
Paarbildung, die nur stattfindet, wenn das Photon genügend Energie besitzt, um ein Elektron-Positron-Paar zu bilden ( $E_{\gamma }$ > 1022 keV).

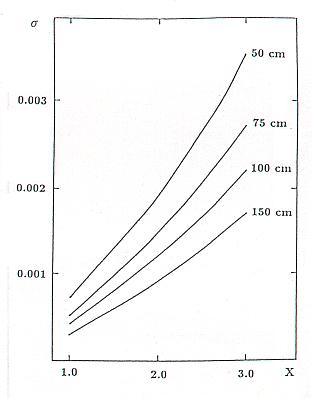
Diese Prozesse haben unterschiedliche Absorptionskoeffizienten, die hauptsächlich vom Energiegehalt der Strahlung, der mittleren Ordnungszahl und der Dichte des Szintillator-Materials abhängen. Allgemein gilt für die Absorption:

I=I_{0}\cdot e^{-\mu d}

wobei $I_{0}$ die Stärke der Strahlung, $d$ die Dicke des Materials und $\mu$ der lineare Absorptionskoeffizient ist, der die Summe der Absorptionskoeffizienten der unterschiedlichen Bestandteile ist:

\mu =\mu _{pe} \mu _{cs} \mu _{pp} \mu _{oc}

Photoelektrischer Effekt: Bei Röntgenstrahlung niedrigerer Energie ( $E_{\gamma }\lesssim$ 60 keV) dominiert der Photoelektrische Effekt. Hierbei werden die Photonen komplett von gebundenen Elektronen des Materials absorbiert, üblicherweise Elektronen der K- und L-Schalen, die in der Folge das Atom verlassen und dieses dadurch ionisieren. Der lineare Absorptionskoeffizient des Photoelektrischen Effekts ist:

\mu _{pe}\propto {\frac {\rho Z^{n}}{E_{\gamma }^{3{,}5}}}

wobei $\rho$ die Dichte des Szintillators, $Z$ die mittlere Ordnungszahl, $n$ eine Konstante, die zwischen 3 und 4 liegt, und $E_{\gamma }$ die Energie des Photons ist. Um einen hohen Wirkungsgrad zu erzielen, werden für Röntgenstrahlung niedriger Energie Szintillatoren aus Atomen höherer Ordnungszahlen und Dichte bevorzugt.

Compton-Effekt: Bei Strahlung höherer Energie ( $E_{\gamma }\gtrsim$ 60 keV) überwiegt der Compton-Effekt, der inelastischen Streuung von Photonen an gebundenen Elektronen, die ebenfalls häufig zur Ionisation führt. Der lineare Absorptionskoeffizient der Compton-Streuung ist:

\mu _{cs}\propto {\frac {\rho }{\sqrt {E_{\gamma }}}}

Anders als beim Photoelektrischen Effekt ist der Compton-Effekt nicht von der Ordnungszahl des Atoms, sondern nur von deren Dichte abhängig.

Paarbildung: Bei Gammastrahlung größer $E_{\gamma }$ > 1022 keV, d. h. bei Energien größer als der doppelten Ruheenergie der Elektronen, kommt es zur Paarbildung. Paarbildung ist das relativistische Phänomen, bei dem die Energie eines Photons in ein Elektron-Positron-Paar umgewandelt wird. Die hierbei entstandenen Elektronen und Positronen reagieren weiter mit dem Szintillator und erzeugen energetische Elektronen und Löcher. Der lineare Absorptionskoeffizient der Paarbildung ist:

\mu _{pp}\propto \rho Z\ln \left({\frac {2E_{\gamma }}{m_{e}c^{2}}}\right)

wobei $m_{e}$ die Ruheenergie des Elektrons und $c$ die Lichtgeschwindigkeit ist. Folglich hängt die Absorption energiereicher Gamma-Strahlung von der Dichte und der mittleren Ordnungszahl des Szintillator-Materials ab. Anders als beim Photo- und Compon-Effekt wird die Wahrscheinlichkeit der Paarbildung mit zunehmender Energie größer und die Paarbildung wird der dominierende Effekt über $E_{\gamma }$ ~ 8 MeV.

Der Term $\mu _{oc}$ beinhaltet andere (kleinere) Beiträge, wie Rayleigh-Streuung bei niedrigeren Energien und Kernphotoeffekte bei sehr großen Energien, die auch zur Wechselwirkung beitragen. Der Effekt der Rayleigh-Streuung kann allerdings vernachlässigt werden und der Kernphotoeffekt tritt nur bei extrem großen Energien auf.

Nachdem die Energie des Ereignisses absorbiert und in sogenannte heiße (hot) Elektronen und Löcher umgewandelt worden ist, reagieren diese mit anderen Teilchen und Quasiteilchen des Szintillators (Elektronen, Plasmons, Phononen). Dieses führt zu einer Art Lawineneffekt, bei dem eine große Zahl sekundärer Elektronen-Löcher-Paare erzeugt werden, bis die „heißen“ Elektronen und Löcher ausreichend Energie verloren haben. Die bei diesem Prozess entstehende große Zahl von Ladungsträgern werden danach „thermalisiert“: sie durchlaufen eine Equilibrierung, d. h., sie geben ihre Energie durch Wechselwirkung mit Phononen (bei Elektronen) bzw. dem Auger-Meitner-Effekt (bei Löchern) des Szintillators ab.

Die mittlere Zeitdauer der Wechselwirkung von der Energieaufnahme bis zur Equilibrierung liegt überschlägig in der Größenordnung einer Pikosekunde ( $10^{-12}$ s), was wesentlich schneller ist als die Abklingzeit von Photolumineszenz.

Transport von angeregten Ladungsträgern

Die zweite Stufe der Szintillation ist der Ladungstransport von thermalisierten Elektronen und Löchern zum Lumineszenz-Zentrum und der Energietransfer zu den Atomen, die in den Lumineszenz-Prozess involviert sind. In dieser Stufe wandert die große Zahl der beim Wechselwirkungs-Prozess entstandenen Elektronen und Löcher innerhalb der Substanz. Dieses ist eine kritische Phase der Szintillation, weil bei diesem Schritt große Verluste durch Einfangen von Elektronen und Löchern in Verunreinigungen, Gitterfehlern und Korngrenzen oder nicht-strahlende Rekombination auftreten können.

Lumineszenz

In der letzten Stufe der Szitillation erreichen die Elektronen und Löcher das Lumineszenz-Zentrum. Hier rekombinieren die positiven und negativen Ladungsträger unter Abgabe von Photonen. Die genaue Art der Rekombination in dieser Phase ist abhängig vom Szintillator-Material.

Szintillatoren

Anorganische Kristalle

In Kristallen, die mit Aktivator-Zentren dotiert sind, erzeugt ionisierende Strahlung freie Elektronen, Löcher oder Elektron-Loch-Paare. Diese wandern im Kristallgitter und regen ein Aktivatorzentrum, wenn sie auf eines treffen, an. Dieses fällt dann unter Emission von sichtbarem Licht (Photonen) wieder in den Grundzustand zurück.

Organische Szintillatoren

In organischen Molekülen entsteht Szintillation durch Doppelbindung von Atomen. Organische Substanzen bilden Kristalle, bei denen die Moleküle durch Van-der-Waals-Kräfte relativ schwach verbunden sind. Der Grundzustand von Kohlenstoff ¹²C ist 1s² 2s² 2p². Wenn Kohlenstoff Verbindungen eingeht, ist nach der Valenzbindungstheorie ein 2s-Elektron angeregt in den 2p-Zustand übergegangen. Dadurch ergibt sich folgende Konfiguration: 1s² 2s¹ 2p³.

Um die unterschiedlichen Wertigkeiten von Kohlenstoff zu beschreiben, wird für die vier möglichen Bindungs-Elektronen-Orbitale (ein 2s und drei 2p) angenommen, dass sie in verschiedenen Konfigurationen hybridisieren können.

Bei der Diamant-Struktur z. B. bilden das s- und die drei p³-Orbitale vier energetisch gleichwertige sp³-Orbitale in tetraedrischer Form. Bei der Graphit-Struktur sind nur zwei der 3 p-Orbitale an der Hybridisierung beteiligt. Die 3 entstehenden sp2-Orbitale richten sich in einer Ebene aus. Die Elektronen dieser Ebene werden σ-Elektronen genannt und Bindungen mit ihnen σ-Bindung. Die übrig gebliebenen p-Orbitale wechselwirken ebenfalls miteinander, allerdings mit deutlich geringer Bindungsenergie. Diese bilden ober- und unterhalb der σ-Bindungsebene ein sogenanntes Elektronengas in Form atomrumpfunabhängiger („delokalisierter“) π-Elektronen. Eine π-Bindung entsteht, wenn zwei π-Orbitale wechselwirken. Das geschieht, wenn ihre Knotenebenen koplanar liegen. Bei derartigen Molekülen können die delokalisierten π-Elektronen durch Strahlung angeregt werden. Beim Rückfall in den energieärmeren Zustand (Abregung) erzeugen die π-Elektronen Lumineszenz.

Die Aufnahme von Strahlung bewirkt eine Anregung in den S₁-Singulett-Zustand. Die beim folgenden Rückfall in den S₀-Zustand abgegebene Strahlung ist Fluoreszenz. Dieses entspricht der schnellen Komponente des Zerfallsprozesses. Die Elektronen können auch Triplett-Zustände annehmen, deren Zerfallszeit deutlich länger ist als die der Singulett-Zustände. Abhängig von der Energie, die die einfallenden Teilchen abgeben (dE/dx), werden unterschiedliche Anteile von „schnellen“ und „langsamen“ Zuständen angenommen. Die relativen Stärke des jeweils abgegebenen Lichts beim Rückfall ist abhängig von der Art des auslösenden Teilchens. D. h., aus der Pulsform des Szintillator-Ausgangssignals lässt sich die Art des auslösenden Teilchens bestimmen.